First a disclaimer: I am no expert on this problem.. I heard it awhile ago, liked it, wrote it down, and that's what you see here. However, I do believe it is still open. If my understanding is correct, the problem considered in the paper you mention ("Efficient approximation algorithms for the subset-sums equality problem" by Bazgan, Santha and Tuza, JCSS Vol.64 Issue 2, March 2002) is a relaxed version of the one stated here where the restriction is not present, and the goal is to find a pair of nonempty disjoint subsets so that and are as close as possible. I believe the only hardness results they obtain are for this problem.
The thing still missing is what to do with the funny assumption . Although the problem is a search problem which looks roughly like a knapsack-type problem (and thus should be NP-hard), the associated decision problem is trivially "true", yet there is no obvious way to use this information.
I think it is still open
First a disclaimer: I am no expert on this problem.. I heard it awhile ago, liked it, wrote it down, and that's what you see here. However, I do believe it is still open. If my understanding is correct, the problem considered in the paper you mention ("Efficient approximation algorithms for the subset-sums equality problem" by Bazgan, Santha and Tuza, JCSS Vol.64 Issue 2, March 2002) is a relaxed version of the one stated here where the restriction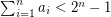 is not present, and the goal is to find a pair of nonempty disjoint subsets
is not present, and the goal is to find a pair of nonempty disjoint subsets 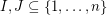 so that
so that  and
and 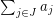 are as close as possible. I believe the only hardness results they obtain are for this problem.
are as close as possible. I believe the only hardness results they obtain are for this problem.
The thing still missing is what to do with the funny assumption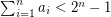 . Although the problem is a search problem which looks roughly like a knapsack-type problem (and thus should be NP-hard), the associated decision problem is trivially "true", yet there is no obvious way to use this information.
. Although the problem is a search problem which looks roughly like a knapsack-type problem (and thus should be NP-hard), the associated decision problem is trivially "true", yet there is no obvious way to use this information.
PS: thanks for the post!