 login/create account
login/create account
 and for every vertex
and for every vertex 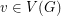 a subset
a subset 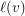 of
of 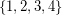 , and decides if there exists a partition of
, and decides if there exists a partition of 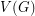 into
into 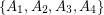 so that
so that 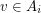 only if
only if 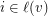 and so that
and so that 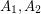 are independent,
are independent, 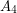 is a clique, and there are no edges between
is a clique, and there are no edges between 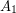 and
and 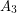 ?
? List partition problems form a very general framework for graph partitioning algorithms. Let  be a symmetric
be a symmetric 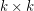 matrix over the alphabet
matrix over the alphabet 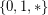 . An
. An  -partition of a graph
-partition of a graph  is a collection of pairwise disjoint sets
is a collection of pairwise disjoint sets 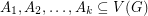 with union
with union 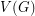 with the following properties. For every
with the following properties. For every 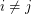 , there are no edges between
, there are no edges between 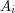 and
and 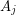 if
if 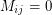 , and all possible edges between
, and all possible edges between 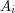 and
and 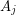 if
if 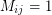 . Similarly, for every
. Similarly, for every 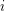 , the set
, the set 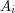 is independent if
is independent if 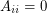 and a clique if
and a clique if 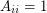 . This framework captures a number of interesting problems. For instance, 3-colorability and skew-partitions are represented by the following matrices.
. This framework captures a number of interesting problems. For instance, 3-colorability and skew-partitions are represented by the following matrices. ![\[ \left[ \begin{array}{ccc} 0 & * & * <br> * & 0 & * <br> * & * & 0 \end{array} \right] \quad\quad\quad \left[ \begin{array}{cccc} * & 1 & * & * <br> 1 & * & * & * <br> * & * & * & 0 <br> * & * & 0 & * \end{array} \right] \]](/files/tex/9737e1c43405b9823d64dce9ae4b44f18252d296.png) So, a graph has an
So, a graph has an  -partition for the first matrix above if and only if it is 3-colorable, and it has a skew partition if and only if it has an
-partition for the first matrix above if and only if it is 3-colorable, and it has a skew partition if and only if it has an  -partition for the second matrix above with the added constraint that
-partition for the second matrix above with the added constraint that 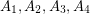 are all nonempty.
are all nonempty.
An even more general framework than  -partitions is list
-partitions is list  -partitions. Here, in addition to a
-partitions. Here, in addition to a 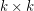 matrix
matrix  , each vertex
, each vertex  of the input graph comes with a list
of the input graph comes with a list 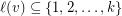 of permitted sets. A solution to this problem is an
of permitted sets. A solution to this problem is an  -partition
-partition 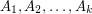 with the added property that whenever
with the added property that whenever 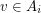 we must have
we must have 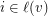 . List
. List  -partition problems arise naturally when studying
-partition problems arise naturally when studying  -partitions, since if we decide to put a particular vertex
-partitions, since if we decide to put a particular vertex  into a particular set, this will generally place some restrictions on the neighbors and nonneighbors of
into a particular set, this will generally place some restrictions on the neighbors and nonneighbors of  which can be encoded by lists.
which can be encoded by lists.
So now, for every possible symmetric 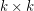 matrix
matrix  (over
(over 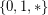 ) we have a decision problem. Namely, given a graph
) we have a decision problem. Namely, given a graph  with a list
with a list 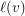 for each vertex
for each vertex 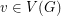 , does
, does  have a list
have a list  -partition? This problem is quite well understood for matrices of size
-partition? This problem is quite well understood for matrices of size 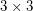 and smaller. Here, every such problem is known to either be polynomial solvable, or be NP-complete. In general, Feder and Hell have proven a kind of quasi-dichotomy result for list partition problems. Namely, every such problem is either NP-complete or has a quasi-polynomial time algorithm (
and smaller. Here, every such problem is known to either be polynomial solvable, or be NP-complete. In general, Feder and Hell have proven a kind of quasi-dichotomy result for list partition problems. Namely, every such problem is either NP-complete or has a quasi-polynomial time algorithm ( 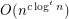 where
where  is the number of vertices, and
is the number of vertices, and 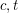 are constants depending only on the matrix). Cameron et all investigated the
are constants depending only on the matrix). Cameron et all investigated the 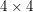 matrices and were able to classify all of the associated list partition problems as either polynomial solvable or NP-complete with the exception of two. One is the stubborn problem, specified by the matrix below (and given in the problem statement), the other is the complementary problem (replace
matrices and were able to classify all of the associated list partition problems as either polynomial solvable or NP-complete with the exception of two. One is the stubborn problem, specified by the matrix below (and given in the problem statement), the other is the complementary problem (replace  's by
's by 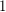 's and
's and 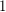 's by
's by  's).
's). ![\[ \left[ \begin{array}{cccc} 0 & * & 0 & * <br> * & 0 & * & * <br> 0 & * & * & * <br> * & * & * & 1 \end{array} \right] \]](/files/tex/2bfc0d518e27ecc8fdc75c1f458c4ab4c09d9860.png) Hell has mentioned to me (M. DeVos) that he believes this stubborn problem to be the tip of a very interesting iceberg, and he suggested the following problem which is closely related, but perhaps better behaved (it is certainly more symmetric).
Hell has mentioned to me (M. DeVos) that he believes this stubborn problem to be the tip of a very interesting iceberg, and he suggested the following problem which is closely related, but perhaps better behaved (it is certainly more symmetric).
Problem: Does there exist a polynomial time algorithm which takes as input a complete graph 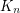 with a (not necessarily proper) edge-coloring
with a (not necessarily proper) edge-coloring 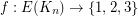 and decides if there exists a vertex coloring
and decides if there exists a vertex coloring 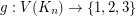 so that no edge
so that no edge 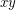 has the same color as both
has the same color as both  and
and 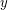 ?
?
Bibliography
[CEHS] K. Cameron, E. Eschen, C.T. Hoàng, R. Sritharan The list partition problem for graphs
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University