I like thinking about this problem in terms of fractional colourings. A roughly equivalent proof (to the one you mentioned) is as follows. In a fractional 3-edge-colouring, every matching must be a perfect matching. The weights on the matchings, when divided by 3, give you a probability distribution. If you pick matchings from this distribution, the union bound tells you that with positive probability you hit every edge. This method is powerful enough to prove that the fractional and integer chromatic numbers are always within a factor of of one another.
Here are two even weaker questions:
Is there some such that any bridgeless cubic graph contains perfect matchings whose intersection does not contain an odd cut?
Does every bridgeless cubic graph contain two perfect matchings that together hit no 5-cut 8 or 10 times?
login/create account
Drupal
CSI of Charles University
Matchings and odd cuts
I like thinking about this problem in terms of fractional colourings. A roughly equivalent proof (to the one you mentioned) is as follows. In a fractional 3-edge-colouring, every matching must be a perfect matching. The weights on the matchings, when divided by 3, give you a probability distribution. If you pick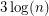
matchings from this distribution, the union bound tells you that with positive probability you hit every edge. This method is powerful enough to prove that the fractional and integer chromatic numbers are always within a factor of 
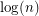of one another.
Here are two even weaker questions:
Is there some
such that any bridgeless cubic graph contains 
perfect matchings whose intersection does not contain an odd cut?
Does every bridgeless cubic graph contain two perfect matchings that together hit no 5-cut 8 or 10 times?
I suspect both of these are open as well.