 login/create account
login/create account
sphere
The Double Cap Conjecture ★★
Author(s): Kalai
Conjecture The largest measure of a Lebesgue measurable subset of the unit sphere of 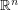 containing no pair of orthogonal vectors is attained by two open caps of geodesic radius
containing no pair of orthogonal vectors is attained by two open caps of geodesic radius 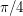 around the north and south poles.
around the north and south poles.
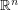 containing no pair of orthogonal vectors is attained by two open caps of geodesic radius
containing no pair of orthogonal vectors is attained by two open caps of geodesic radius 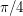 around the north and south poles.
around the north and south poles. Keywords: combinatorial geometry; independent set; orthogonality; projective plane; sphere
Smooth 4-dimensional Poincare conjecture ★★★★
Author(s): Poincare; Smale; Stallings
Conjecture If a 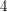 -manifold has the homotopy type of the
-manifold has the homotopy type of the 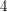 -sphere
-sphere 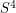 , is it diffeomorphic to
, is it diffeomorphic to 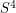 ?
?
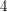 -manifold has the homotopy type of the
-manifold has the homotopy type of the 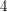 -sphere
-sphere 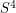 , is it diffeomorphic to
, is it diffeomorphic to 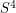 ?
?
Keywords: 4-manifold; poincare; sphere
Smooth 4-dimensional Schoenflies problem ★★★★
Author(s): Alexander
Problem Let  be a
be a  -dimensional smooth submanifold of
-dimensional smooth submanifold of 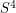 ,
,  diffeomorphic to
diffeomorphic to 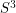 . By the Jordan-Brouwer separation theorem,
. By the Jordan-Brouwer separation theorem,  separates
separates 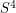 into the union of two compact connected
into the union of two compact connected 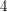 -manifolds which share
-manifolds which share  as a common boundary. The Schoenflies problem asks, are these
as a common boundary. The Schoenflies problem asks, are these 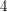 -manifolds diffeomorphic to
-manifolds diffeomorphic to 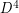 ? ie: is
? ie: is  unknotted?
unknotted?
 be a
be a  -dimensional smooth submanifold of
-dimensional smooth submanifold of 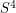 ,
,  diffeomorphic to
diffeomorphic to 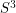 . By the Jordan-Brouwer separation theorem,
. By the Jordan-Brouwer separation theorem,  separates
separates 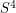 into the union of two compact connected
into the union of two compact connected 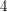 -manifolds which share
-manifolds which share  as a common boundary. The Schoenflies problem asks, are these
as a common boundary. The Schoenflies problem asks, are these 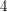 -manifolds diffeomorphic to
-manifolds diffeomorphic to 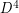 ? ie: is
? ie: is  unknotted?
unknotted? Keywords: 4-dimensional; Schoenflies; sphere

 Drupal
Drupal CSI of Charles University
CSI of Charles University