 login/create account
login/create account
reloid
Distributivity of outward reloid over composition of funcoids ★★
Author(s): Porton
Keywords: distributive; distributivity; funcoid; functor; outward reloid; reloid
Funcoid corresponding to inward reloid ★★
Author(s): Porton
Keywords: funcoid; inward reloid; reloid
Monovalued reloid is a restricted function ★★
Author(s): Porton
Conjecture If a reloid is monovalued then it is a monovalued function restricted to some filter.
Keywords: monovalued morphism; monovalued reloid; reloid

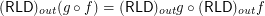 for any composable
for any composable  and
and 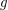 .
. 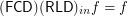 for any
for any 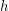 are
are 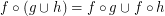 ; \item
; \item 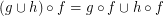 .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University