 login/create account
login/create account
Shannon capacity of the seven-cycle
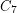 ?
?
Let 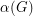 denote the independence number of the graph
denote the independence number of the graph  , and let
, and let 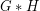 denote the strong graph product of
denote the strong graph product of  and
and  (in which
(in which 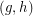 is adjacent to
is adjacent to 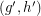 if
if 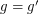 and
and 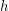 is adjacent to
is adjacent to 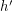 , or if
, or if 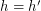 and
and  is adjacent to
is adjacent to 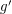 , or if
, or if  is adjacent to
is adjacent to 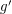 and
and 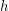 is adjacent to
is adjacent to 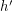 ). Then the Shannon capacity of
). Then the Shannon capacity of  is defined by
is defined by 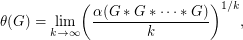 where the strong graph product is over
where the strong graph product is over  copies of
copies of  . The Shannon capacity is important because it represents the effective size of an alphabet in a communication model represented by
. The Shannon capacity is important because it represents the effective size of an alphabet in a communication model represented by  , but it is notoriously difficult to compute. Lovász [L] famously proved that the Shannon capacity of the five-cycle
, but it is notoriously difficult to compute. Lovász [L] famously proved that the Shannon capacity of the five-cycle 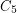 is
is 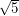 , but even the Shannon capacity of
, but even the Shannon capacity of 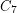 remains unknown. However, Bohman [B] has shown that
remains unknown. However, Bohman [B] has shown that 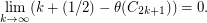
Bibliography
[B] Tom Bohman, A limit theorem for the Shannon capacity of odd cycles II, Proc. Amer. Math. Soc. 133 (2005), no. 2, 537-543.
[L] László Lovász, On the Shannon capacity of a graph, IEEE Trans. Inform. Th. IT-25 (1979), 1-7.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University