Home » Subject » Number Theory
Importance: High ✭✭✭
Author(s): Buchholz, Ralph H.
MacDougall, James A.
Subject: Number Theory
Keywords: derivative
diophantine
elliptic
polynomial
Recomm. for undergrads: no
Posted by: mdevos
on: May 17th, 2008

Call a polynomial $ p \in {\mathbb Q}[x] $ rationally derived if all roots of $ p $ and the nonzero derivatives of $ p $ are rational.

Conjecture   There does not exist a quartic rationally derived polynomial $ p \in {\mathbb Q}[x] $ with four distinct roots.

Probably anyone who has ever designed simple problems for calculus students has looked for polynomials $ p $ with the property that both $ p $ and some small derivatives of it are easy to factor. Perhaps inspired by this, Buchholz and MacDougall attempted to classify all univariate polynomials defined over a domain $ k $ with the property that they and all their nonzero derivatives have all their roots in $ k $. 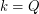This problem can be split into cases dependent upon the multiplicity of the roots, and Buchholz and MacDougall solved many of the small ones for $ k={\mahtbb Q} $. 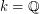Based on their results and a theorem of Flynn [F], an affirmative solution to the above conjecture would complete this classification problem for $ k={\mathbb Q} $.

Bibliography

*[BM] R. Buchholz, and J. MacDougall, When Newton met Diophantus: a study of rational-derived polynomials and their extension to quadratic fields. J. Number Theory 81 (2000), no. 2, 210--233. MathSciNet

[F] E. V. Flynn, On Q-derived polynomials. Proc. Edinb. Math. Soc. (2) 44 (2001), no. 1, 103--110. MathSciNet


* indicates original appearance(s) of problem.
1 comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options