Open Problem Garden

Importance: High ✭✭✭

Author(s):

Subject:	Number Theory
	» Combinatorial Number Theory

Keywords:

subset sum

Recomm. for undergrads: no

Prize: $500 (Erdos-Graham)

Posted	by:	mdevos
	on:	June 24th, 2007

Say that a set 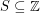$S \subseteq {\mathbb Z}$ has distinct subset sums if distinct subsets of $S$ have distinct sums.

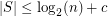Conjecture There exists a fixed constant $c$ so that $|S| \le \log_2(n) + c$ whenever 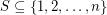$S \subseteq \{1,2,\ldots,n\}$ has distinct subset sums.

Erdos valued this problem at $500, and I (M. DeVos) believe these prizes are now supported by Ron Graham.

Define the function 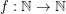$f : {\mathbb N} \rightarrow {\mathbb N}$ by the rule $f(n) = \min \{ \max S : S \subseteq {\mathbb N} \mbox{ has distinct subset sums and } |S| = n \}$

Then Erdos' conjecture is equivalent to the assertion that 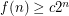$f(n) \ge c 2^n$ for a fixed constant $c$ , and more generally, we would like to understand the behavior of $f$ .

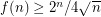Erdos and Moser established an upper bound on $f$ , proving that $f(n) \ge 2^n / 4 \sqrt{n}$ . This was later improved by a constant factor by Elkies [E].

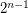We get an easy lower bound on $f$ by observing that the set $S$ consisting of the first $n$ powers of 2 has distinct subset sums, and has maximal element $2^{n-1}$ . This shows that 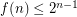$f(n) \le 2^{n-1}$ . At first glance, it might appear that such sets are optimal, but these sets have too many small numbers, and it is possible to improve upon them. Conway and Guy [CG] found a construction of sets with distinct subset sum, now called the Conway-Guy sequence, which gives an interesting upper bound on $f$ . This was this was later improved by Lunnan [L], and then by Bohman [B] to 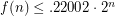$f(n) \le .22002 \cdot 2^n$ (for $n$ sufficiently large).

Bibliography

[B] T. Bohman, A construction for sets of integers with distinct subset sums, The Electronic. Journal of Combinatorics 5 (1998) /#R3

[CG] J. H. Conway and R. K. Guy, Sets of natural numbers with distinct subset sums, Notices, Amer. Math. Soc., 15 (1968) 345.

[E] N. Elkies, An improved lower bound on the greatest element of a sum-distinct set of fixed order, J. Comb. Th. A, 41 (1986) 89-94.

[G1] R. K. Guy, Sets of integers whose subsets have distinct sums, Ann. Discrete Math., 12 (1982) 141-154.

[G2] R. K. Guy, Unsolved Problems in Number Theory, Springer-Verlag, 1981.

[L] W. F. Lunnon, Integers sets with distinct subset sums, Math. Compute, 50 (1988) 297-320.

* indicates original appearance(s) of problem.

1 comment

Open Problem Garden

Bibliography

Reply

Navigate

Recent Activity