 login/create account
login/create account
 is a connected graph on
is a connected graph on  vertices, then
vertices, then 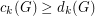 for
for 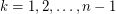 .
. (Reproduced from [M].)
Let 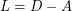 be the Laplacian matrix of a graph
be the Laplacian matrix of a graph  of order
of order  . Let
. Let 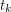 be the
be the  -th largest eigenvalue of
-th largest eigenvalue of 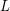 (
(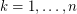 ). For the purpose of this problem, we call the number
). For the purpose of this problem, we call the number 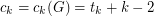 the
the  -th Laplacian degree of
-th Laplacian degree of  . In addition to that, let
. In addition to that, let 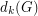 be the
be the  -th largest (usual) degree in
-th largest (usual) degree in  . It is known that every connected graph satisfies
. It is known that every connected graph satisfies 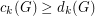 for
for 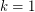 [GM],
[GM], 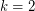 [LP] and for
[LP] and for 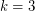 [G].
[G].
Bibliography
[GM] R. Grone, R. Merris, The Laplacian spectrum of a graph II, SIAM J. Discrete Math.7 (1994) 221-229. MathSciNet
[LP] J.S. Li, Y.L. Pan, A note on the second largest eigenvalue of the Laplacian matrix of a graph, Linear Multilin. Algebra 48 (2000) 117-121. MathSciNet
*[G] J.-M. Guo, On the third largest Laplacian eigenvalue of a graph, Linear Multilin. Algebra 55 (2007) 93-102. MathSciNet
[M] B. Mohar, Problem of the Month
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University