 login/create account
login/create account
Definition Let 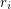 be the unique integer (with respect to a fixed
be the unique integer (with respect to a fixed 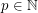 ) such that
) such that
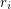 be the unique integer (with respect to a fixed
be the unique integer (with respect to a fixed 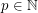 ) such that
) such that
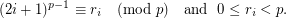
Conjecture A natural number 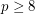 is a prime iff
is a prime iff ![$$ \displaystyle \sum_{i=1}^{\left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor} r_i = \left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor $$](/files/tex/99af565f4cc4d3bab11eb3fbf54f78626678d484.png)
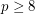 is a prime iff
is a prime iff ![$$ \displaystyle \sum_{i=1}^{\left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor} r_i = \left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor $$](/files/tex/99af565f4cc4d3bab11eb3fbf54f78626678d484.png)
The conjecture is obviously true when  is prime, so it suffices to check when
is prime, so it suffices to check when  is composite.
is composite.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University