Home » Subject » Geometry
Importance: Medium ✭✭
Author(s):
Subject: Geometry
Keywords: complete geometric graph, edge colouring
Recomm. for undergrads: no
Posted by: David Wood
on: October 19th, 2009
Conjecture   Every complete geometric graph with an even number of vertices has a partition of its edge set into plane (i.e. non-crossing) spanning trees.

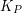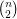For a set $ P $ of $ n $ points in the plane with no three collinear, the complete geometric graph $ K_P $ has vertex set $ P $ and edge set consisting of the $ \binom{n}{2} $ straight line-segments between each pair of points in $ P $.

Since each subtree of 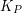$ K_P $ has at most 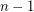$ n-1 $ edges, every partition of 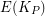$ E(K_P) $ into subtrees has at least 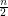$ \frac{n}{2} $ parts. The conjecture asks for such a partition into exactly 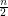$ \frac{n}{2} $ subtrees, such that in addition, no two edges in each subtree cross.

It is folklore that the conjecture is true if $ P $ is in convex partition. In fact, the edge set of the complete convex graph can be partitioned into plane Hamiltonian paths. Bose et al. [BHRW] characterised all possible partitions of the complete convex graph into plane spanning trees. Bose et al. 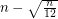[BHRW] also proved that every complete geometric graph on $ n $ vertices can be partitioned into at most $ n-\sqrt{\frac{n}{12}} $ plane subtrees.

I heard about this conjecture from Ferran Hurtado in 2003, but the problem is much older than that.

Related problems

Edge-Colouring Geometric Complete Graphs

Bibliography

[BHRW] Prosenjit Bose, Ferran Hurtado, Eduardo Rivera-Campo, David R. Wood. Partitions of complete geometric graphs into plane trees, Computational Geometry: Theory & Applications 34(2):116-125, 2006. MathSciNet


* indicates original appearance(s) of problem.
1 comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options