 login/create account
login/create account
A regular graph  is strongly regular if there exist integers
is strongly regular if there exist integers 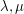 so that every pair of adjacent vertices have exactly
so that every pair of adjacent vertices have exactly 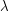 common neighbors, and every pair of nonadjacent vertices have exactly
common neighbors, and every pair of nonadjacent vertices have exactly 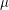 common neighbors. To eliminate degeneracies, we shall further assume that
common neighbors. To eliminate degeneracies, we shall further assume that 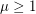 . If
. If  is
is  -regular and
-regular and 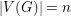 , then we say that
, then we say that  is a
is a 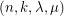 strongly regular graph.
strongly regular graph.
There are exactly seven triangle-free strongly regular graphs known: The five cycle, the Petersen Graph, The Clebsch Graph, the Hoffman-Singleton Graph, The Gewirtz Graph, the Higman-Sims Graph, and a 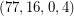 strongly regular subgraph of the Higman-Sims graph. Every Moore Graph of diameter 2 is a triangle-free strongly regular graph, so if there is a 57-regular Moore Graph of diameter 2, this would add another to the list.
strongly regular subgraph of the Higman-Sims graph. Every Moore Graph of diameter 2 is a triangle-free strongly regular graph, so if there is a 57-regular Moore Graph of diameter 2, this would add another to the list.
See Andries Brouwer's graph descriptions for more on these graphs.
Bibliography
[G] C. D. Godsil, Problems in Algebraic Combinatorics, Electronic Journal of Combinatorics, Volume 2, F1
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University