 login/create account
login/create account
Call a graph an 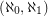 -graph if it has a bipartition
-graph if it has a bipartition 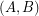 so that every vertex in
so that every vertex in  has degree
has degree 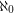 and every vertex in
and every vertex in 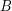 has degree
has degree 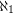 .
.
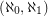 -graphs.
-graphs. The motivation for this problem comes from a lovely paper of Diestel and Leader [DL] where they prove that an infinite graph has a normal spanning tree (the natural infinite analogue of a depth-first search tree) if and only if it has no minor isomorphic to either an 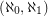 -graph or an Aronszajn tree. (An earlier conjecture of Halin asserted that only the first of these excluded minors was needed.) So,
-graph or an Aronszajn tree. (An earlier conjecture of Halin asserted that only the first of these excluded minors was needed.) So, 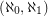 -graphs appear as a forbidden minor obstruction to the existence of a kind of depth-first search tree for infinite graphs.
-graphs appear as a forbidden minor obstruction to the existence of a kind of depth-first search tree for infinite graphs.
The obvious example of an 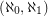 -graph is
-graph is 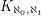 , but there are other natural families of such graphs. For instance, let
, but there are other natural families of such graphs. For instance, let  be an infinite binary tree with root
be an infinite binary tree with root  , and let
, and let 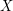 be the set of all rays (one way infinite paths) with endpoint
be the set of all rays (one way infinite paths) with endpoint  . Now, form a bipartite graph with vertex bipartition
. Now, form a bipartite graph with vertex bipartition 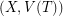 and adjacency given by the rule that
and adjacency given by the rule that 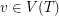 adjacent to
adjacent to 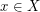 if and only if
if and only if  lies on the ray
lies on the ray  (in
(in  ). Any
). Any 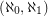 -graph which is isomorphic to a subgraph of this graph is said to be of binary type.
-graph which is isomorphic to a subgraph of this graph is said to be of binary type.
Say that a 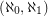 -graph is divisible if there exist disjoint subsets
-graph is divisible if there exist disjoint subsets 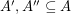 and disjoint subsets
and disjoint subsets 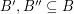 so that the graphs induced by both
so that the graphs induced by both 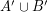 and
and 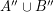 are
are 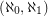 -graphs. It is not difficult to show that every binary type graph is divisible. Curiously, the existence of non-divisible
-graphs. It is not difficult to show that every binary type graph is divisible. Curiously, the existence of non-divisible 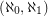 -graphs depends on the Continuum Hypothesis (see [DL]).
-graphs depends on the Continuum Hypothesis (see [DL]).
Although it is not clear wether or not there is a nice characterization of 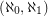 -graphs, it would certainly be interesting to find more natural families of these graphs. The following rather more concrete question is posed by Diestel and Leader who suspect the answer is 'no'.
-graphs, it would certainly be interesting to find more natural families of these graphs. The following rather more concrete question is posed by Diestel and Leader who suspect the answer is 'no'.
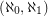 -graph have an
-graph have an 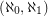 -graph as a minor which is either indivisible or of binary type?
-graph as a minor which is either indivisible or of binary type? Bibliography
[DL] R. Diestel and I. Leader, Normal spanning trees, Aronszajn trees and excluded minors, J. London Math. Soc. 63 (2001), 16-32;
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University