 login/create account
login/create account
 is a bridgeless cubic graph, then there exist 6 perfect matchings
is a bridgeless cubic graph, then there exist 6 perfect matchings 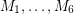 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 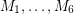 .
.
This conjecture is due to Berge and Fulkerson, and appears first in [F] (see [S79b]).
If  is 3-edge-colorable, then we may choose three perfect matchings
is 3-edge-colorable, then we may choose three perfect matchings 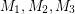 so that every edge is in exactly one. Taking each of these twice gives us 6 perfect matchings with the properties described above. Thus, the above conjecture holds trivially for 3-edge-colorable graphs. There do exist bridgeless cubic graphs which are not 3-edge-colorable (for instance the Petersen graph), but the above conjecture asserts that every such graph is close to being 3-edge-colorable.
so that every edge is in exactly one. Taking each of these twice gives us 6 perfect matchings with the properties described above. Thus, the above conjecture holds trivially for 3-edge-colorable graphs. There do exist bridgeless cubic graphs which are not 3-edge-colorable (for instance the Petersen graph), but the above conjecture asserts that every such graph is close to being 3-edge-colorable.
Definition: An  -graph is an
-graph is an  -regular graph
-regular graph  on an even number of vertices with the property that every edge-cut which separates
on an even number of vertices with the property that every edge-cut which separates 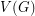 into two sets of odd cardinality has size at least
into two sets of odd cardinality has size at least  .
.
Observe that a cubic graph is a 3-graph if and only if it has no bridge. If G is an  -regular graph which has an
-regular graph which has an  -edge-coloring, then every color class is a perfect matching, so
-edge-coloring, then every color class is a perfect matching, so 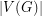 must be even, and every color must appear in every edge-cut which separates
must be even, and every color must appear in every edge-cut which separates 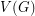 into two sets of odd size, so every edge-cut of this form must have size at least
into two sets of odd size, so every edge-cut of this form must have size at least  . Thus, every
. Thus, every  -edge-colorable
-edge-colorable  -regular graph is an
-regular graph is an  -graph. In a sense, we may view the
-graph. In a sense, we may view the  -graphs as the
-graphs as the  -regular graphs which have the obvious necessary conditions to be
-regular graphs which have the obvious necessary conditions to be  -edge-colorable. Seymour [S79b] defined
-edge-colorable. Seymour [S79b] defined  -graphs and offered the following generalization of the Berge-Fulkerson conjecture.
-graphs and offered the following generalization of the Berge-Fulkerson conjecture.
 be an
be an  -graph. Then there exist
-graph. Then there exist 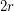 perfect matchings
perfect matchings 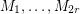 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 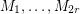 .
. More generally, for a graph 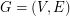 , one may consider the vector space of real numbers indexed by
, one may consider the vector space of real numbers indexed by  . We associate every perfect matching
. We associate every perfect matching  with its characteristic vector. In this context, the Berge-Fulkerson conjecture asserts that for every 3-graph, the vector which is identically 1 may be written as a half-integer combination of perfect matchings. Edmonds matching polytope theorem [E] gives a complete characterization of what vectors in
with its characteristic vector. In this context, the Berge-Fulkerson conjecture asserts that for every 3-graph, the vector which is identically 1 may be written as a half-integer combination of perfect matchings. Edmonds matching polytope theorem [E] gives a complete characterization of what vectors in 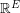 which can be written as a nonnegative real combination of perfect matchings. A particular consequence of this theorem is that the vector which is identically 1 can be written as a nonnegative rational combination of perfect matchings if G is an
which can be written as a nonnegative real combination of perfect matchings. A particular consequence of this theorem is that the vector which is identically 1 can be written as a nonnegative rational combination of perfect matchings if G is an  -graph. It follows from this that for every
-graph. It follows from this that for every  -graph
-graph  , there is a list of perfect matchings
, there is a list of perfect matchings 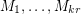 so that every edge is contained in exactly
so that every edge is contained in exactly  of them. Unfortunately, the particular
of them. Unfortunately, the particular  depends on the graph. The following weak version of the Berge-Fulkerson conjecture asserts that this dependence is inessential.
depends on the graph. The following weak version of the Berge-Fulkerson conjecture asserts that this dependence is inessential.
 with the following property. Every 3-graph
with the following property. Every 3-graph  has a list of
has a list of 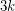 perfect matchings such that every edge of
perfect matchings such that every edge of  is contained in exactly
is contained in exactly  of them.
of them. There is a fascinating theorem of Lovasz [L] that characterizes which vectors in 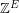 can be written as an integer combination of perfect matchings. However, very little is known about nonnegative integer combinations of perfect matchings. In particular, if the Berge-Fulkerson conjecture is true, then for every 3-graph
can be written as an integer combination of perfect matchings. However, very little is known about nonnegative integer combinations of perfect matchings. In particular, if the Berge-Fulkerson conjecture is true, then for every 3-graph 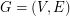 , there is a list of 5 perfect matchings with union
, there is a list of 5 perfect matchings with union  (take any 5 of the 6 perfect matchings given by the conjecture). The following weakening of this (suggested by Berge) is still open.
(take any 5 of the 6 perfect matchings given by the conjecture). The following weakening of this (suggested by Berge) is still open.
 such that the edge set of every 3-graph can be written as a union of
such that the edge set of every 3-graph can be written as a union of  perfect matchings.
perfect matchings. Another consequence of the Berge-Fulkerson conjecture would be that every 3-graph has 3 perfect matchings with empty intersection (take any 3 of the 6 perfect matchings given by the conjecture). The following weakening of this (also suggested by Berge) is still open.
 such that every 3-graph has a list of
such that every 3-graph has a list of  perfect matchings with empty intersection.
perfect matchings with empty intersection. Bibliography
[E] J. Edmonds, Maximum matching and a polyhedron with 0,1-vertices, J. Res. Nat. Bur Stand B, Math & Math Phys. 69B (1965), 125-130.
[F] D.R. Fulkerson, Blocking and anti-blocking pairs of polyhedra, Math. Programming 1 (1971) 168-194. MathSciNet
[KKN] T. Kaiser, D. Kral, and S. Norine, Unions of perfect matchings in cubic graphs
[L] L. Lovasz, Matching structure and the matching lattice, J. Combin. Theory Ser. B 43 (1987), 187-222. MathSciNet
[R] R. Rizzi, Indecomposable r-graphs and some other counterexamples, J. Graph Theory 32 (1999), 1-15. MathSciNet
[S79a] P.D. Seymour, "Some unsolved problems on one-factorizations of graphs", Graph theory and Related Topics, J.A. Bondy and U.S.R. Murty (Editors), Academic, New York (1979), 367-368.
[S79b] P.D. Seymour, On multi-colourings of cubic graphs, and conjectures of Fulkerson and Tutte, Proc. London Math Soc. 38 (1979), 423-460. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University